【完全系ってなに？】音程と度数について

※先に度数について知りたい人は ここ だけ見てください！

みなさんこんにちは。りーほーです。

さて、今回は、 音程 と 度数 について書いてみます。

感覚的に音楽を作っていく上では特に意識しなくても良いかもしれませんが、音楽を掘り下げて考えていく時には必ず考える必要がある２つのワードです。

ぼくも勉強しながら書いてます。数学的な要素もありますがお付き合いください！

音程と度数とは

さっそくですが、音程とは、「２つの音の高さの差」のことです。音程を英語で言うと Interval ( インターバル )です。

ちなみに、よくカラオケなんかで音を外した時に「音程外した〜」とか言いますが、正確に言うとあれは「 音程 」ではなく「 音高 」( Pitch )を外している と言うのが正しいです。音程は２つの音の高低差、音高はその音自体の高さを表しているということですね。

で、音程の差を表す言葉が度数 ( Degree )です。

GarageBandで作曲する上で、音程や度数を意識する必要がある？

ないといえばないし、あるといえばあるでしょう。あくまでGarageBandの機能を用いて、GarageBandの範囲内で作曲するのであれば、知らなくても全然OKです。

なぜなら、GarageBandは理論を意識しなくても楽しく作曲できるように作られているからですね。

ですが、以前にダイアトニックコードの記事でも書きましたが、GarageBandはあくまで足がかりで、GarageBandをキッカケに、超えていってほしいわけですね。

GarageBandをキッカケに、音楽の世界にのめり込んでいって欲しいわけです。

というわけで、今回こんな記事を書いてます。

度数ってなに

では、度数ってなんなんでしょう？

度数とは、例えばドレミの「ド」に対して、「レ」は2度、「ミ」は3度、という感じです。数える起点となる音( ルート音 )から、どれだけ離れているか、どれだけ高さの差があるかを数字で表した表現方法です。これだけみると簡単そうですが、実はそこまで簡単でもありません。

度数の数え方

この2度や3度という数え方には、頭に「長」や「短」などの言葉がつきます。

そう、曲の キー などで使う長調( メジャー )、短調( マイナー )と同じ長短です。

さらに、ここに「完全」、「減」、「増」などという言葉も出てくるのでわからなくなります。

ここでは、まずはこれだけ抑えましょう。

まずはこれだけ。覚えなくてもいいので、こう言う考え方というところだけ、まずは知っておきましょう！

度数の数え方一覧

まずはこちらをご覧ください↓。

これが度数の数え方と、キーがC(ド)の場合の音名です。

完全系である1、4、5、8度には色をつけました。

まず、完全とか増減とか長短ってのがわかりづらいので、考え方を表にしてみました↓。

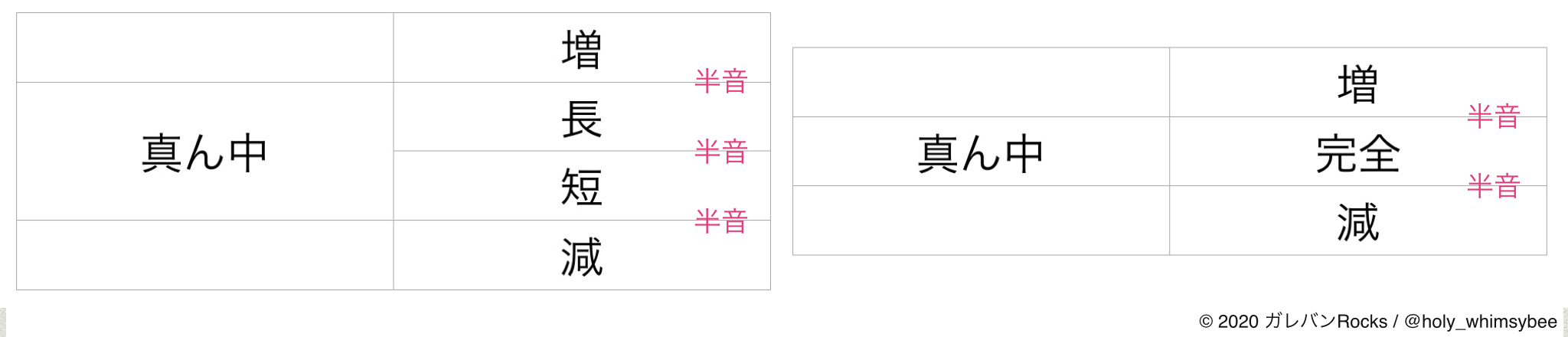
完全はど真ん中で、それに対して半音の上と下が増と減。

対して長短は、合わせてど真ん中で、その半音上と下が増と減。

長短の上下を増減と呼ぶケースはかなり少なそうなので、覚えるのは長短だけでも良いかもです。

長短はそれぞれ「長がルート音に対して明るい音」、「短がルート音に対して暗い音」なのに対し、「完全はそれ自体がルート音と協和する音」です。

完全に対する増減はそれぞれ増＝ オーギュメント ( augment )、減＝ ディミニッシュ ( diminish )と言い、この音を使ったコードは、たとえばCなら増だとCaug、減だとCdimやC♭5といった種類のコードがあります。メジャーやマイナーなどに比べてなかなか使いどころが難しいですが、うまく使うとアクセントになってカッコよくなる事も。

では、なぜ1、4、5、8度が「完全」系なのでしょう…？

1度4度5度8度が「完全」と呼ばれる理由

ここからすこし数学的なお話になります。

1、4、5、8度が「完全」である理由は、ズバリ1度の音と親和性がとっても高いからなんですね。

ここで一つ、↓をご覧ください。

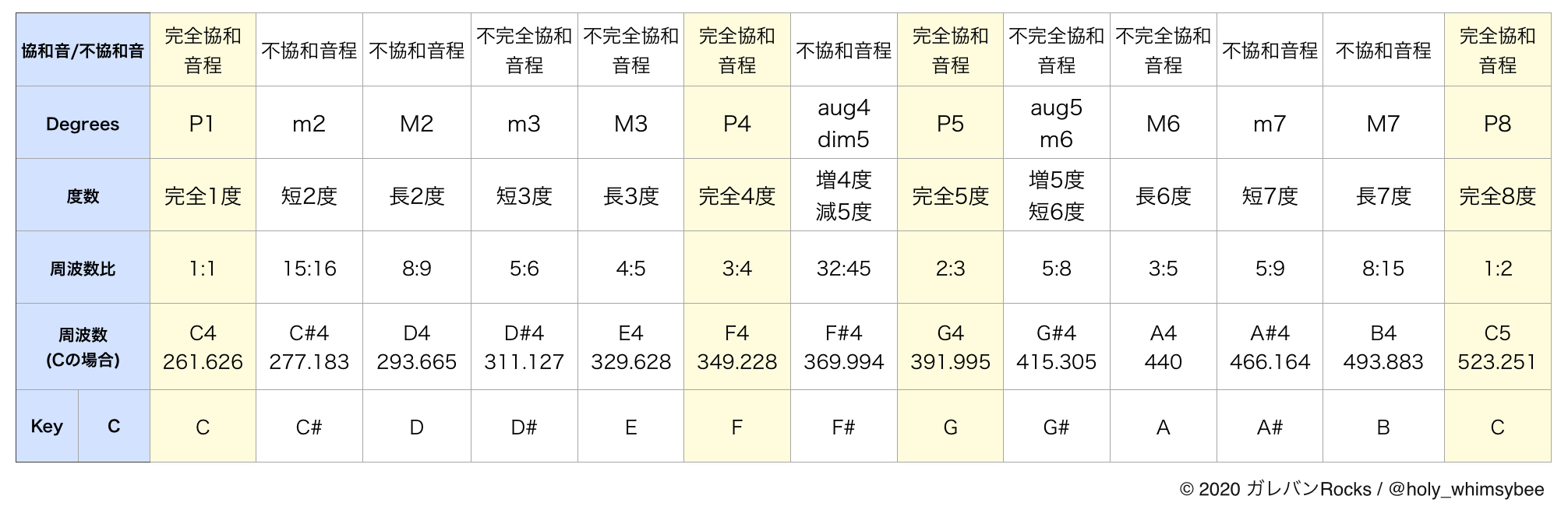
先ほどの図に、さらにそれぞれの音の周波数、1度の音との周波数の比率、協和音であるか否か と言う項目を追加しました。

音 とは、1秒間で空気が振動する回数によって音の高さが変わります。その回数が、イコール 周波数 となるわけです。音が高いほど、1秒間の振動数は大きくなります。

たとえば上の図だと、C4(ピアノで左から数えて4番めのドの音)は、1秒間で261.626回振動しているわけですね。

ここで注目したいのは、ルートである1度の周波数とそれぞれの度数の音の周波数の周波数比です。

1度の音は同じ音なので、周波数も同じ。だから1:1ですね。8度の音は1オクターブ上の音。オクターブ上の音は周波数が2倍なので1:2。

さらに見ると、5度の音は周波数が2:3、4度の音は3:4。ここまでが、1度の音の周波数に対して比率の整数が小さくシンプル、＝ルート音(1度の音)と親和性が高く協和しやすい音、と言うことなのですね。

それ以外の音を見てみると、増4度(減5度)なんかは32:45と、とても相性が悪そうですね…。

この比率が3:4である4度の音までが、とても親和性が高い「完全協和音程」、それ以下が「不完全協和音程」、「不協和音程」と続くわけですね。

協和音程はそのキーに対してマッチしやすい音なので、曲作りの基本となる音やコードです。かたや不協和音程は、そのキーにはマッチしない音です。

が、不協和音程は上手く使うと絶妙にカッコいいフックになったりするので、ぜひ積極的にトライしてみたいですね。

GarageBandでも、コード編集機能で不協和音程を含んだコードを使う事も可能でございます。詳しくはこちら↓。

GarageBand(iOS版)の使い方〜コードの編集の仕方〜

GarageBand(iOS版)のコード編集のやり方について解説しています。Alchemyシンセ、SmartPiano、SmartGuitar、SmartBassにおいて、デフォルトのコードを自分の好きなコードにカスタマイズする方法など。

garageband-rocks.com

2020.02.29

数学しっかりやっておけばよかった

こう言う記事を書いてみると、つくづくこの世は数学でできてるな〜と実感しますね。感覚的に「良い」とか「違和感がある」が、数学で説明できてしまっているわけですから。

生まれ変わったら理系で頑張ります。(バリバリ文系)

ということで今日はこの辺で！

ではまた〜。